«`html
LibMOON: Библиотека градиентного многокритериального оптимизации для масштабного машинного обучения
Многокритериальная оптимизация (MOO) играет ключевую роль в машинном обучении, позволяя исследователям балансировать несколько противоречащих целей в реальных приложениях. Эти приложения включают робототехнику, справедливую классификацию и рекомендательные системы. В таких областях критически важно учитывать компромиссы между показателями производительности, такими как скорость по сравнению с энергоэффективностью в робототехнике или справедливость по сравнению с точностью в моделях классификации. Эти сложные задачи требуют оптимизационных техник, которые одновременно учитывают различные цели, обеспечивая учет каждого фактора в процессе принятия решений.
Проблема многокритериальной оптимизации
Существенной проблемой в многокритериальной оптимизации является необходимость масштабируемых методов для эффективной работы с крупными моделями, содержащими миллионы параметров. В то время как традиционные подходы, особенно эволюционные алгоритмы, могут быть полезны в определенных сценариях, они испытывают затруднения при применении к задачам машинного обучения большого масштаба. Эти методы часто не используют информацию, основанную на градиентах, что критически важно для оптимизации сложных моделей. Без оптимизации на основе градиентов вычислительная нагрузка увеличивается, что делает практически невозможным решение проблем, связанных с глубокими нейронными сетями или другими крупными моделями.
LibMOON: Решение на основе градиентов
Команда исследователей из City University of Hong Kong, SUSTech, HKBU и UIUC представила LibMOON — новую библиотеку, которая решает эту проблему, обеспечивая фреймворк градиентной многокритериальной оптимизации. Реализованная в PyTorch, LibMOON разработана для более эффективной оптимизации крупномасштабных моделей машинного обучения по сравнению с предыдущими методами. Библиотека поддерживает более двадцати передовых методов оптимизации и предлагает ускорение с использованием GPU, что делает ее высокоэффективной для задач крупного масштаба.
Функциональность LibMOON
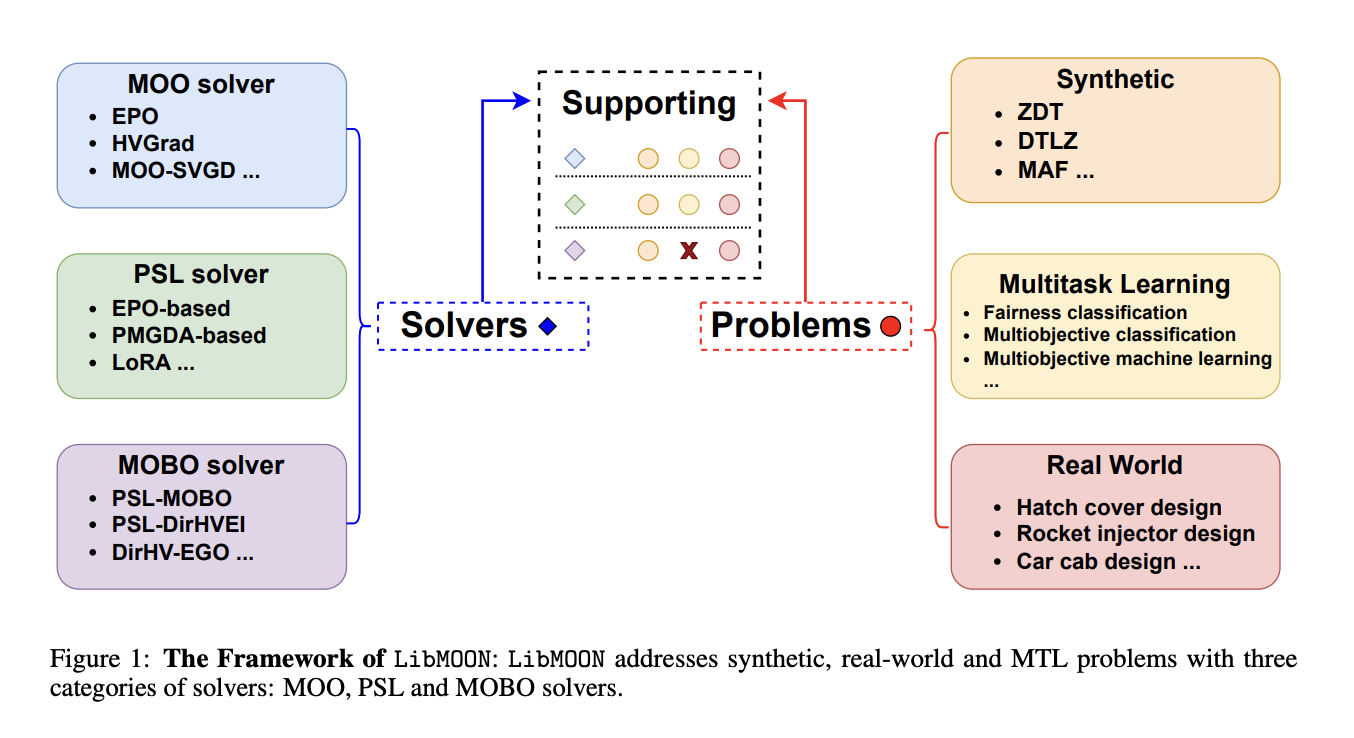
Основу функциональности LibMOON составляют три категории решателей: решатели многокритериальной оптимизации (MOO), решатели обучения множества Парето (PSL) и решатели байесовской многокритериальной оптимизации (MOBO). Каждая из этих категорий решателей модульна и позволяет легко интегрировать новые методы, что делает LibMOON высокоадаптивной. Решатели MOO направлены на поиск конечного набора Парето-оптимальных решений. В отличие от этого, решатели PSL нацелены на представление всего множества Парето с использованием одной нейронной модели. Метод PSL особенно полезен для оптимизации моделей с миллионами параметров, поскольку он уменьшает необходимость нахождения нескольких решений и вместо этого одновременно обучает целое множество Парето-оптимальных решений. Решатели MOBO предназначены для решения дорогостоящих задач оптимизации, где оценка целевых функций затратна. Эти решатели используют передовые методы байесовской оптимизации для уменьшения количества оценок функций, что делает их идеальными для реальных приложений, где ограничены вычислительные ресурсы.
Результаты и применение
LibMOON демонстрирует впечатляющую производительность при решении различных оптимизационных задач, превзойдя традиционные эволюционные подходы. Библиотека поддерживает как синтетические, так и реальные многокритериальные задачи, а также позволяет проводить обширное тестирование, обеспечивая исследователей надежной платформой для сравнения и разработки.
Библиотека также поддерживает решение реальных задач, таких как справедливая классификация и многокритериальные задачи машинного обучения. В тестах LibMOON превзошла существующие методы, достигнув более высоких показателей гиперобъема и разнообразия, и снизив вычислительное время.
В заключение, LibMOON представляет собой надежное градиентное решение для многокритериальной оптимизации, решая ключевые ограничения существующих методов. Его способность эффективно масштабироваться к крупным моделям машинного обучения и обеспечивать точные множества Парето делает его неотъемлемым инструментом для исследователей в области машинного обучения.
«`