«`html
DeepSPoC: Интеграция Sequential Propagation of Chaos с глубоким обучением для эффективного решения среднепольных стохастических дифференциальных уравнений
Недавно была разработана техника Sequential Propagation of Chaos (SPoC) для решения среднепольных стохастических дифференциальных уравнений (SDE) и их связанных нелинейных уравнений Фоккера-Планка. Эти уравнения описывают эволюцию вероятностных распределений под воздействием случайного шума и являются важными в таких областях, как динамика жидкости и биология.
Традиционные методы решения этих уравнений сталкиваются с проблемами из-за их нелинейности и высокой размерности. Методы частиц, которые аппроксимируют решения с помощью взаимодействующих частиц, предлагают преимущества перед методами на основе сетки, но требуют больших вычислительных мощностей и занимают много места в памяти.
Недавние достижения в области глубокого обучения, такие как физически информированные нейронные сети, предлагают многообещающую альтернативу. Вопрос возникает: можно ли объединить методы частиц с глубоким обучением, чтобы преодолеть их соответствующие ограничения.
Решение
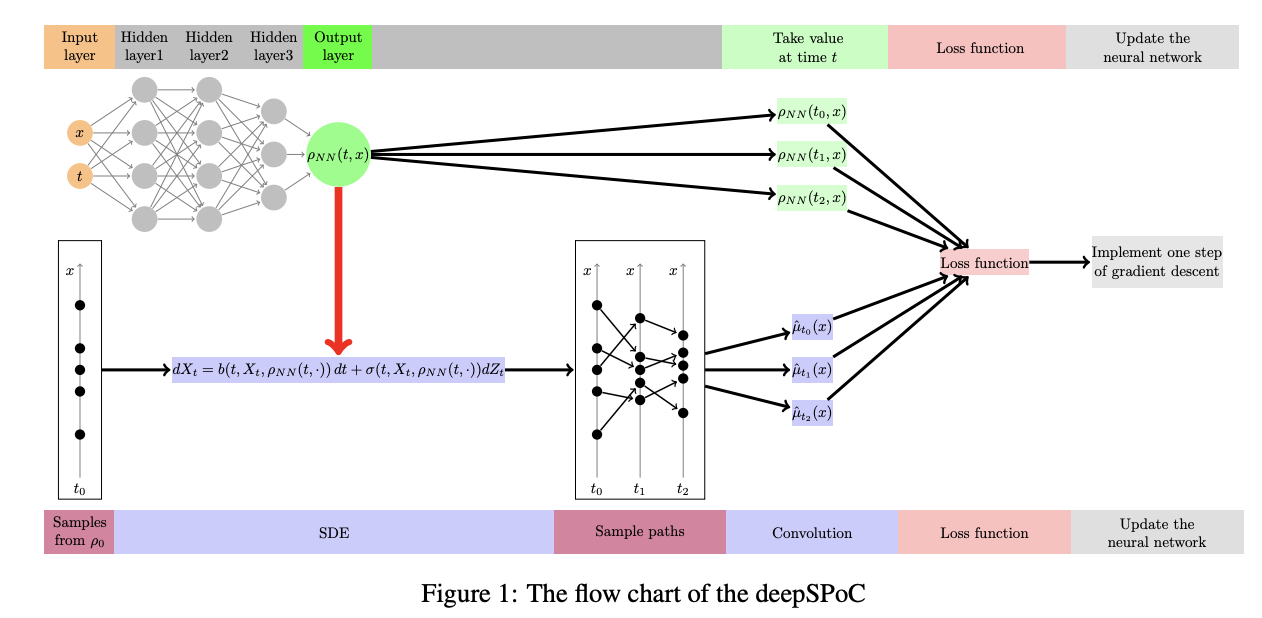
Исследователи из Шанхайского центра математических наук и Китайской академии наук разработали новый метод под названием deepSPoC, который интегрирует SPoC с глубоким обучением. Этот подход использует нейронные сети, такие как полностью связанные сети и нормализующие потоки, для приближения эмпирического распределения частиц, тем самым устраняя необходимость хранения больших траекторий частиц.
Метод deepSPoC улучшает точность и эффективность для задач высокой размерности, адаптируясь пространственно и используя итерационный подход к пакетному моделированию. Теоретический анализ подтверждает его сходимость и оценку ошибки. Исследование демонстрирует эффективность deepSPoC на различных уравнениях среднего поля, выделяя его преимущества в экономии памяти, вычислительной гибкости и применимости к задачам высокой размерности.
Преимущества deepSPoC
Алгоритм deepSPoC улучшает метод SPoC, интегрируя техники глубокого обучения. Он приближает решение среднепольных SDE, используя нейронные сети для моделирования временно-зависимой плотности функции взаимодействующей системы частиц. DeepSPoC включает в себя моделирование динамики частиц с помощью решателя SDE, вычисление эмпирических мер и уточнение параметров нейронной сети с помощью градиентного спуска на основе функции потерь.
Нейронные сети могут быть как полностью связанными, так и нормализующими потоками, с соответствующими функциями потерь L^2-расстояния или KL-дивергенции. Этот подход улучшает масштабируемость и эффективность при решении сложных уравнений в частных производных.
Теоретический анализ и численные эксперименты
Теоретический анализ алгоритма deepSPoC первоначально рассматривает его свойства сходимости при использовании базисных функций Фурье для приближения функций плотности вместо нейронных сетей. Это включает исправление аппроксимаций, чтобы убедиться, что они являются действительными вероятностными плотностями. Анализ показывает, что при достаточно больших базисных функциях Фурье приближенная плотность близко соответствует истинной плотности, и сходимость алгоритма может быть строго доказана. Кроме того, анализ включает оценку ошибки, демонстрируя, насколько близким является численное решение к истинному путем сравнения плотности решения с точной, используя метрики, такие как расстояние Вассерштейна и Hα.
Исследование оценивает алгоритм deepSPoC через различные численные эксперименты, включающие среднепольные SDE с различными пространственными размерностями и формами b и sigma. Исследователи тестируют deepSPoC на уравнениях пористой среды (PME) различных размеров, включая 1D, 3D, 5D, 6D и 8D, сравнивая его производительность с детерминированными методами частиц и используя полностью связанные нейронные сети и нормализующие потоки. Результаты демонстрируют, что deepSPoC эффективно обрабатывает эти уравнения, улучшая точность со временем и решая задачи высокой размерности с разумной точностью.
Заключение
Вводится алгоритмическая структура для решения нелинейных уравнений Фоккера-Планка, используя полностью связанные сети, KRnet и различные функции потерь. Эффективность этой структуры демонстрируется через различные численные примеры, с теоретическим доказательством сходимости с использованием базисных функций Фурье. Анализируется оценка ошибки, показывающая, что адаптивный метод улучшает точность и эффективность для задач высокой размерности. Будущая работа направлена на расширение этой структуры на более сложные уравнения, такие как нелинейные уравнения Власова-Пуассона-Фоккера-Планка, и на проведение дальнейшего теоретического анализа архитектуры сети и функций потерь. Кроме того, предлагается и тестируется deepSPoC, который объединяет SPoC с глубоким обучением, на различных среднепольных уравнениях.
Проверьте статью. Вся заслуга за это исследование принадлежит исследователям этого проекта.
Не забудьте следить за нами в Twitter и LinkedIn. Присоединяйтесь к нашему каналу в Telegram. Если вам нравится наша работа, вам понравится наша рассылка.
Не забудьте присоединиться к нашему SubReddit по машинному обучению с более чем 50 тысячами подписчиков.
Попробуйте ИИ ассистент в продажах здесь. Этот ИИ ассистент в продажах помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж и снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с решениями от Flycode.ru.