Исследование Sharpness-Aware Minimization (SAM): Особенности устойчивости к помехам меток и обобщению
Недавно возрос интерес к улучшению обобщения глубоких сетей путем регулирования остроты функции потерь. Sharpness Aware Minimization (SAM) стал популярен благодаря своей выдающейся производительности на различных бенчмарках, особенно в управлении случайными помехами меток, превосходя SGD на значительные отрезки. Устойчивость SAM проявляется особенно в случаях помех меток, демонстрируя существенные улучшения по сравнению с существующими техниками. Кроме того, эффективность SAM сохраняется даже при недопараметризации, что потенциально увеличивает выгоду от больших наборов данных. Понимание поведения SAM, особенно на ранних этапах обучения, становится ключевым для оптимизации его производительности.
Практические применения
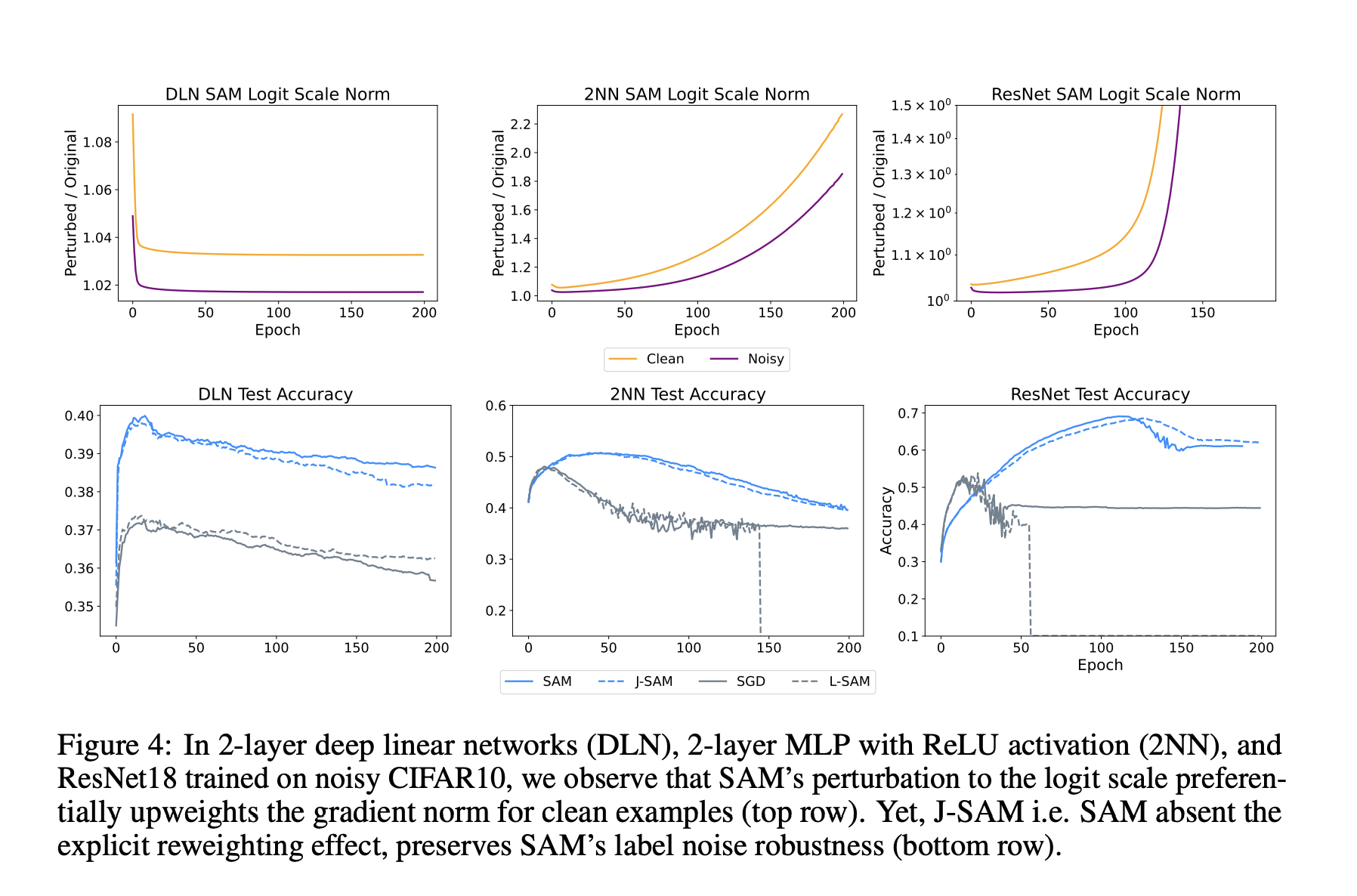
Экспериментальные исследования на игрушечных данных Гаусса с помехами меток показывают, что SAM демонстрирует значительно более высокую точность тестирования на ранних этапах по сравнению с SGD. Анализируя процесс обновления SAM, становится очевидно, что его адверсариальная пертурбация весов приоритетно увеличивает сигнал градиента от точек с низкими потерями, тем самым поддерживая высокий вклад чистых примеров на ранних этапах обучения. Этот предпочтительный характер для чистых данных приводит к более высокой точности тестирования до переобучения на помехи. Исследование также проливает свет на роль логит-шкалы SAM, показывая, как она эффективно увеличивает градиенты от точек с низкими потерями, в конечном итоге улучшая общую производительность.
В заключение, данная работа направлена на предоставление надежной перспективы эффективности SAM, демонстрируя его способность приоритизировать обучение на чистых примерах перед подгонкой к шумным, особенно в присутствии помех меток. В линейных моделях SAM явно увеличивает градиенты от точек с низкими потерями, аналогично существующим методам устойчивости к помехам меток. В нелинейных средах регулирование SAM промежуточных активаций и весов последнего слоя улучшает устойчивость к помехам меток, подобно методам, регулирующим норму логитов. Несмотря на их сходства, SAM остается недостаточно изученным в области помех меток. Тем не менее, симулирование аспектов регуляции SAM сетевым Якобианом может сохранить его производительность, предлагая потенциал для разработки методов устойчивости к помехам меток, вдохновленных принципами SAM, несмотря на дополнительные временные затраты 1-SAM.