«`html
Революционное доказательство теорем: как синтетические доказательства изменяют возможности LLM
Доказательные ассистенты, такие как Lean, обеспечивают высокую точность в математических доказательствах, решая растущую сложность современной математики, которая часто приводит к ошибкам. Формальные языки, такие как Lean, Isabelle и Coq, создают компьютерно-проверяемые доказательства, но требуют значительных усилий и экспертизы. Автоматизированное доказательство теорем становится все более важным, с новыми методами, фокусирующимися на алгоритмах поиска потенциальных решений. Несмотря на улучшения в LLM, этим методам требуется больше обучающих данных. Продвижение в автоформализации предлагает определенное облегчение, но наборы данных остаются слишком маленькими, чтобы полностью использовать возможности LLM.
Практические решения и ценность
Исследователи из DeepSeek, Университета Сунь Ят-сен, Университета Эдинбурга и MBZUAI разработали метод генерации обширных данных доказательств LFourfour из задач математических соревнований старших классов и студентов. Путем перевода этих задач в формальные утверждения, фильтрации низкокачественных и генерации доказательств они создали набор данных из 8 миллионов утверждений. Путем настройки модели DeepSeekMath 7B на этих данных им удалось достичь точности 46,3% в генерации полного доказательства на тесте Lean 4 miniF2F, превзойдя 23,0% у GPT-4. Их модель также решила 5 из 148 задач бенчмарка FIMO, превзойдя GPT-4. Эта работа продвигает доказательство теорем путем использования синтетических данных большого масштаба.
Автоматизированное доказательство теорем (ATP) является ключевой областью исследований в области искусственного интеллекта с момента своего возникновения. Оно развилось от эффективных доказателей первого порядка, таких как E и Vampire, к обработке сложных теорем в современных доказательственных ассистентах, таких как Lean, Isabelle и Coq. Недавние успехи в глубоком обучении и модельно-управляемом поиске возродили ATP, объединяя нейронные модели с алгоритмами поиска в дереве и обучением с подкреплением. Эти методы, хотя и мощные, требуют больших ресурсов. Автоформализация, преобразование естественного языка в формальные утверждения, решает проблему ограниченных обучающих данных. Недавние усилия синтезируют большие наборы формальных доказательств, используя LLM, чтобы значительно улучшить производительность нейронных доказателей на сложных математических задачах.
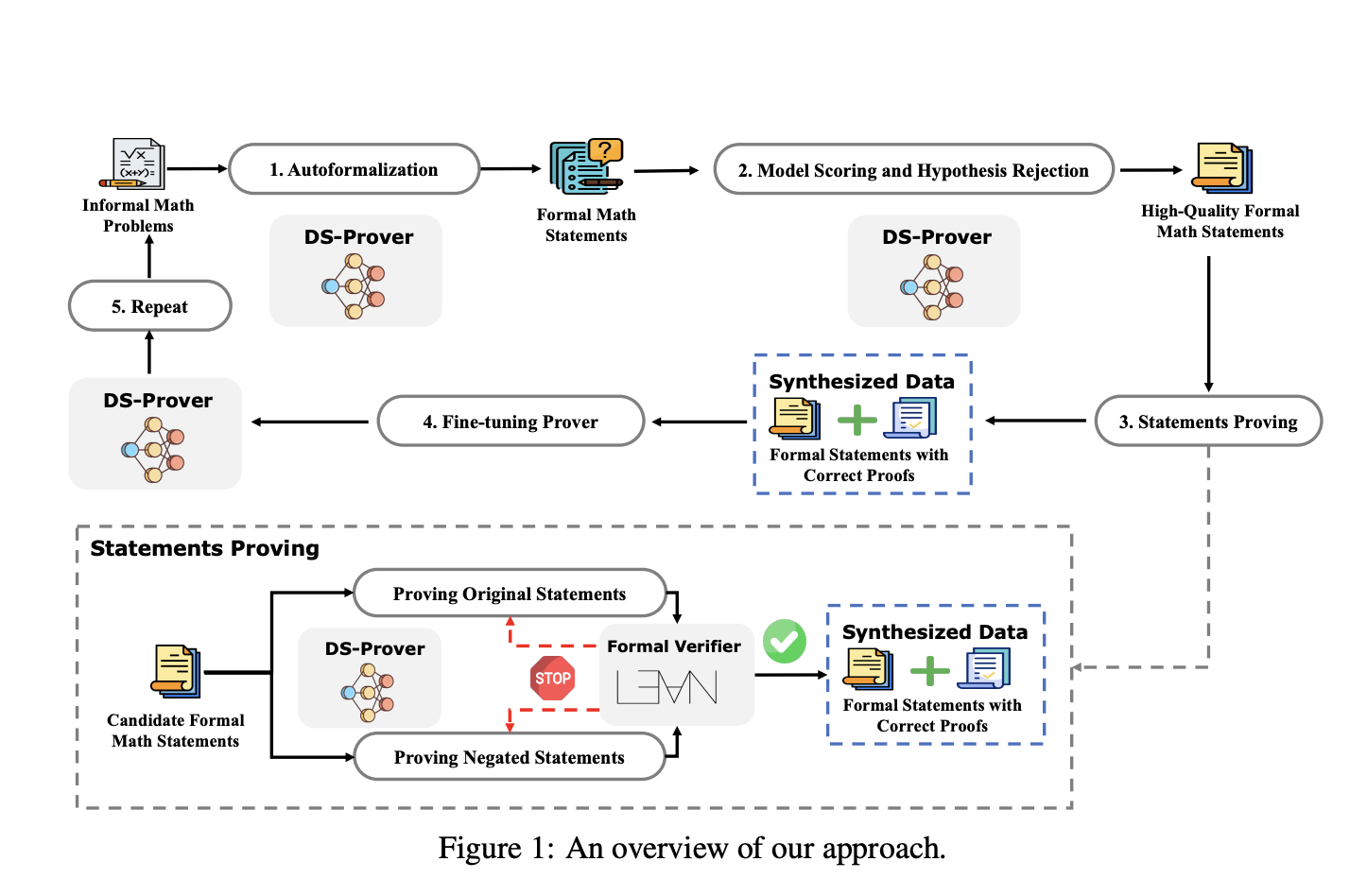
Подход включает четыре основных этапа. Формальные математические утверждения изначально генерируются из большой коллекции неформальных математических задач. Эти автоформализованные утверждения проходят фильтрацию через оценку модели и отклонение гипотез для выбора высококачественных. Затем модель DeepSeek-Prover пытается доказать эти утверждения с проверкой корректности с помощью формального верификатора Lean 4, что приводит к подтвержденным формальным утверждениям и доказательствам. Эти данные используются для настройки модели DeepSeek-Prover, и процесс повторяется, пока улучшения не станут незначительными. Для улучшения эффективности доказательства одновременно доказываются как исходные утверждения, так и их отрицания, быстро отбрасывая недопустимые утверждения.
DeepSeek-Prover, основанный на модели DeepSeekMath-Base 7B, был настроен с глобальным размером пакета 512 и постоянной скоростью обучения 1 × 10^−4, включая 6 000 шагов разогрева с использованием синтетических данных. Его производительность была сравнена с GPT-3.5, GPT-4 и несколькими передовыми методами, такими как GPT-f, Proof Artifact Co-Training, ReProver, Llemma и COPRA. Оценки на бенчмарках miniF2F и FIMO показали, что DeepSeek-Prover превзошел другие, достигнув 60,2% на miniF2F-valid и 52,0% на miniF2F-test, значительно превышая 25,41% и 22,95% у GPT-4. Бенчмарк FIMO успешно доказал пять теорем с разными попытками, превзойдя GPT-4, который не смог установить ни одной.
В заключение, исследование разработало метод генерации обширных синтетических доказательств из задач математических соревнований старших классов и студентов. Путем перевода задач на естественном языке в формальные утверждения, фильтрации низкокачественных данных и использования итеративного доказательства было создано 8 миллионов доказательств, значительно улучшающих производительность модели DeepSeekMath 7B в автоматизированном доказательстве теорем. Модель превосходит GPT-4 и другие бенчмарки, такие как miniF2F и FIMO. Открытые наборы данных и модель направлены на продвижение исследований в области автоматизированного доказательства теорем и улучшение возможностей крупных языковых моделей в формальном математическом рассуждении, с планами расширения области решаемых математических проблем в будущих работах.
«`