«`html
Генерализация градиентного спуска в рекуррентных нейронных сетях с избыточным числом параметров: Инсайты из стабильности минимумов и больших скоростей обучения
Нейронные сети, обученные методом градиентного спуска, эффективно работают даже в переопределенных ситуациях с случайной инициализацией весов, часто находя глобально оптимальные решения, несмотря на не выпуклую природу проблемы. Эти решения, достигающие нулевой ошибки обучения, во многих случаях удивительно не переобучаются, что известно как «благополучное переобучение». Однако для сетей ReLU интерполирующие решения могут привести к переобучению. Более того, лучшие решения обычно не интерполируют данные в сценариях с шумными данными. Практическое обучение часто прекращается до полного интерполяции, чтобы избежать попадания в нестабильные области или решений, которые неустойчивы к шумам.
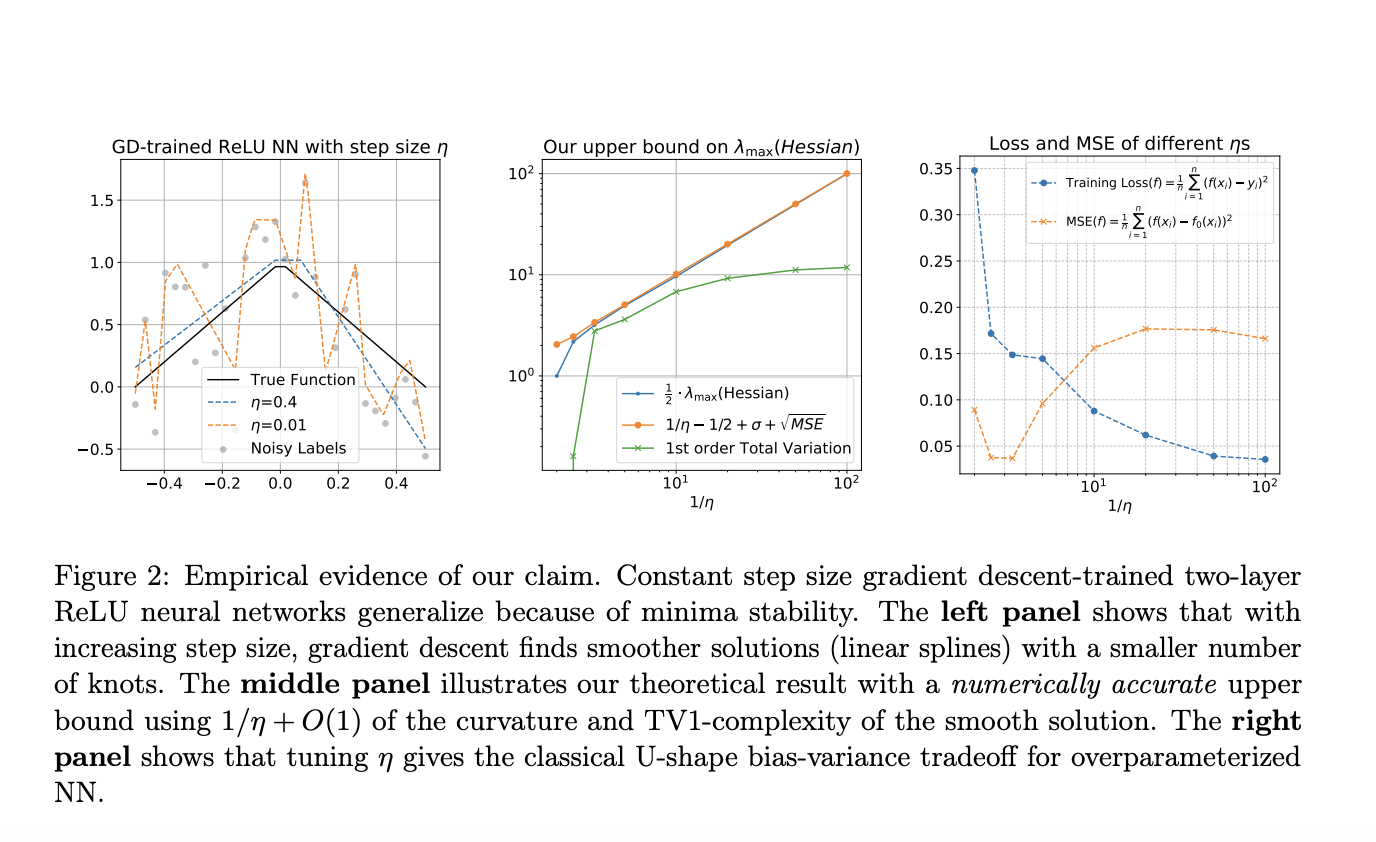
Исследователи из UC Santa Barbara, Technion и UC San Diego исследуют обобщение двухслойных ReLU нейронных сетей в 1D непараметрической регрессии с шумными метками. Они представляют новую теорию, показывающую, что градиентный спуск с фиксированной скоростью обучения сходится к локальным минимумам, представляющим собой гладкие, разреженные линейные функции. Эти решения, которые не интерполируют, избегают переобучения и достигают почти оптимальной среднеквадратической ошибки (MSE). Их анализ подчеркивает, что большие скорости обучения влекут за собой неявную разреженность и что сети ReLU могут хорошо обобщаться даже без явной регуляризации или преждевременной остановки. Эта теория выходит за рамки традиционных ядерных и интерполяционных платформ.
Узнайте, как ИИ может изменить ваши процессы с решениями от Flycode.ru
«`