«`html
Улучшение производительности Kolmogorov-Arnold Networks (KANs) с использованием среднего значения в нейронах
Колмогорово-Арнольдовские сети (KAN) представляют собой многообещающую альтернативу традиционным многослойным перцептронам (MLP). Они используют нейроны, выполняющие простые операции сложения, вдохновленные теоремой представления Колмогорова-Арнольда. Однако текущая реализация KAN создает некоторые вызовы в практических приложениях. Исследователи в настоящее время изучают возможность идентификации альтернативных многомерных функций для нейронов KAN, которые могли бы предложить улучшенную практическую ценность в рамках нескольких задач машинного обучения.
Практическое применение
Исследования выявили потенциал KAN в различных областях, таких как компьютерное зрение, анализ временных рядов и поиск квантовой архитектуры. Некоторые исследования показывают, что KAN может превзойти MLP в задачах подгонки данных и решении уравнений в частных производных, используя меньшее количество параметров. Однако некоторые исследования вызывают опасения относительно устойчивости KAN к шуму и их производительности по сравнению с MLP. Также исследуются вариации и улучшения стандартной архитектуры KAN, такие как графовые конструкции, сверточные KAN и основанные на трансформаторах KAN для решения этих проблем. Кроме того, исследуются альтернативные функции активации, такие как вейвлеты, радиальные базисные функции и синусоидальные функции, для улучшения эффективности KAN. Несмотря на эти работы, существует необходимость в дальнейших улучшениях для повышения производительности KAN.
Предложенное усовершенствование
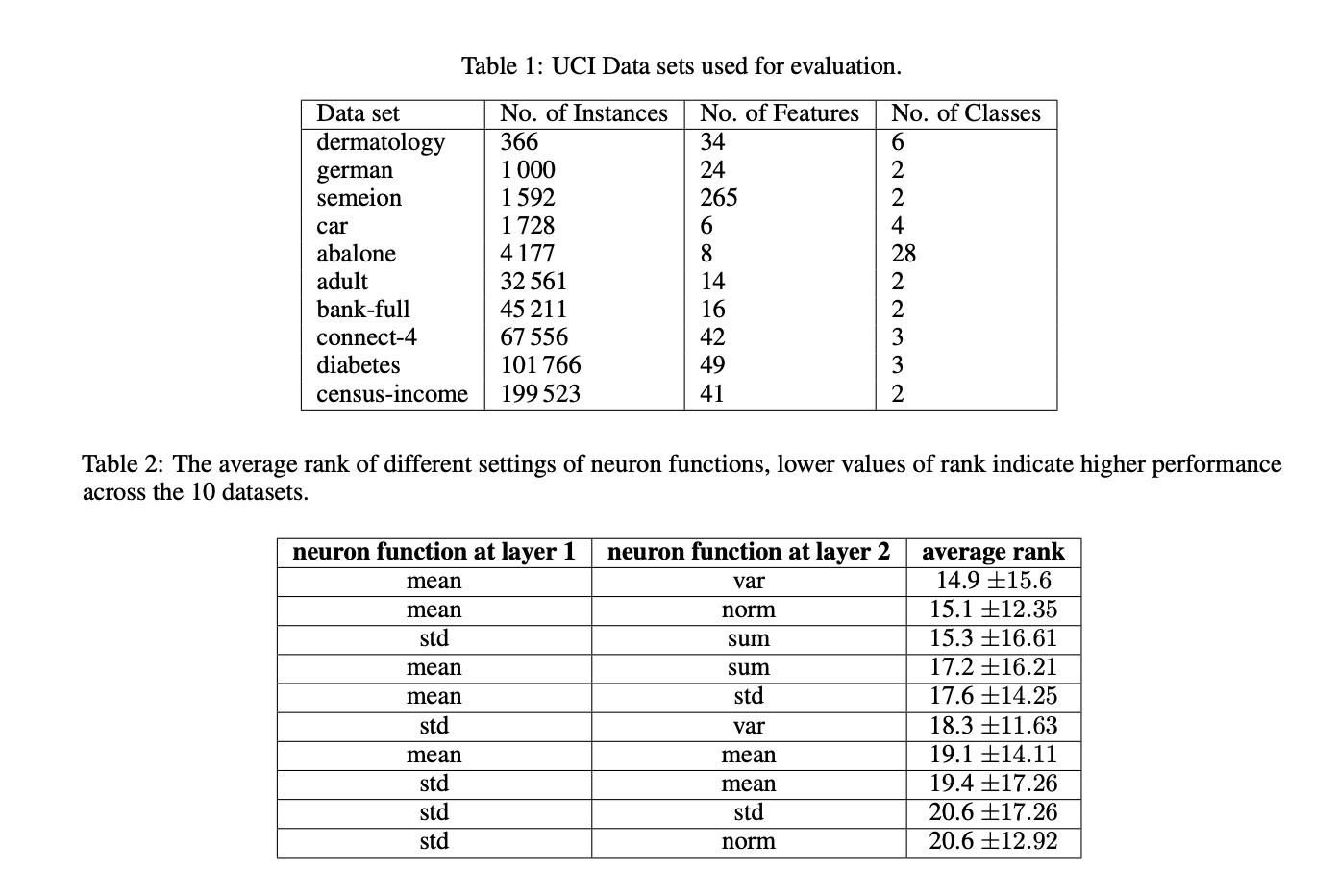
Исследователь из Центра исследований прикладных интеллектуальных систем Хальмстадского университета (Швеция) предложил новый подход для улучшения производительности Kolmogorov-Arnold Networks (KAN). Этот метод направлен на определение оптимальной многомерной функции для нейронов KAN в различных задачах классификации машинного обучения. Традиционное использование сложения в качестве функции уровня узла часто неидеально, особенно для высокоразмерных наборов данных с множеством признаков. Это может привести к превышению входных значений эффективного диапазона последующих функций активации, что приводит к нестабильности обучения и снижению обобщающей способности. Для решения этой проблемы исследователь предлагает использовать среднее значение вместо суммы в качестве функции узла.
Результаты и перспективы
Проведенные эксперименты показали, что использование среднего значения в нейронах KAN эффективнее, чем традиционная сумма. Это улучшение обусловлено способностью среднего значения поддерживать входные значения в оптимальном диапазоне функции активации сплайнов, который составляет [-1.0, +1.0]. Стандартные KAN испытывали затруднения с поддержанием значений в этом диапазоне в промежуточных слоях при увеличении количества признаков. Однако использование среднего значения в нейронах приводит к улучшению производительности, поддерживая значения в желаемом диапазоне на наборах данных с 20 и более признаками. Для наборов данных с меньшим количеством признаков значения оставались в диапазоне более 99,0% времени, за исключением набора данных «abalone», у которого немного ниже уровень соблюдения — 96,51%.
Эти исследования предлагают многообещающее направление для будущих реализаций KAN, потенциально улучшая их производительность и применимость в различных задачах машинного обучения.
«`