«`html
Преодоление евклидовой парадигмы: план развития машинного обучения с геометрическими, топологическими и алгебраическими структурами
Этот материал обсуждает ограничения классических подходов к машинному обучению, разработанных преимущественно для данных, лежащих в евклидовом пространстве. Современное машинное обучение все чаще сталкивается с богато структурированными данными, которые по своей сути не являются евклидовыми, проявляя сложные геометрические, топологические и алгебраические структуры. Извлечение знаний из таких неевклидовых данных требует более широкого математического взгляда, чем традиционная евклидова модель.
Решения и практическое применение
Традиционные методы машинного обучения, созданные преимущественно для евклидова пространства, плохо справляются с данными, обладающими сложными геометрическими, топологическими и алгебраическими структурами, такими как кривизна пространства-времени или нейронные связи в мозге. Известно, что геометрия евклидова не может адекватно описать изогнутые пространства общей теории относительности или сложные взаимосвязанные структуры нейронных сетей. С учетом этого ограничения возникла область геометрического глубокого обучения, которая стремится расширить классические методы машинного обучения на неевклидовы области, используя геометрические, топологические и алгебраические структуры.
Команда исследователей из Университета Калифорнии, Санта-Барбара, Atmo, Inc, New Theory AI, Universite C´ ote d’Azur & Inria, и Университета Калифорнии, Беркли, предлагает комплексную методологию для современного машинного обучения, интегрирующую неевклидовые геометрии, топологии и алгебраические структуры. Этот подход включает обобщение классических статистических и глубинного обучения для обработки данных, не соответствующих традиционным евклидовым предположениям. Исследователи разработали графическую таксономию, классифицирующую эти современные методы, облегчающую понимание их применений и взаимосвязей. Эта таксономия уточняет существующие методы и выделяет области для будущих исследований и развития.
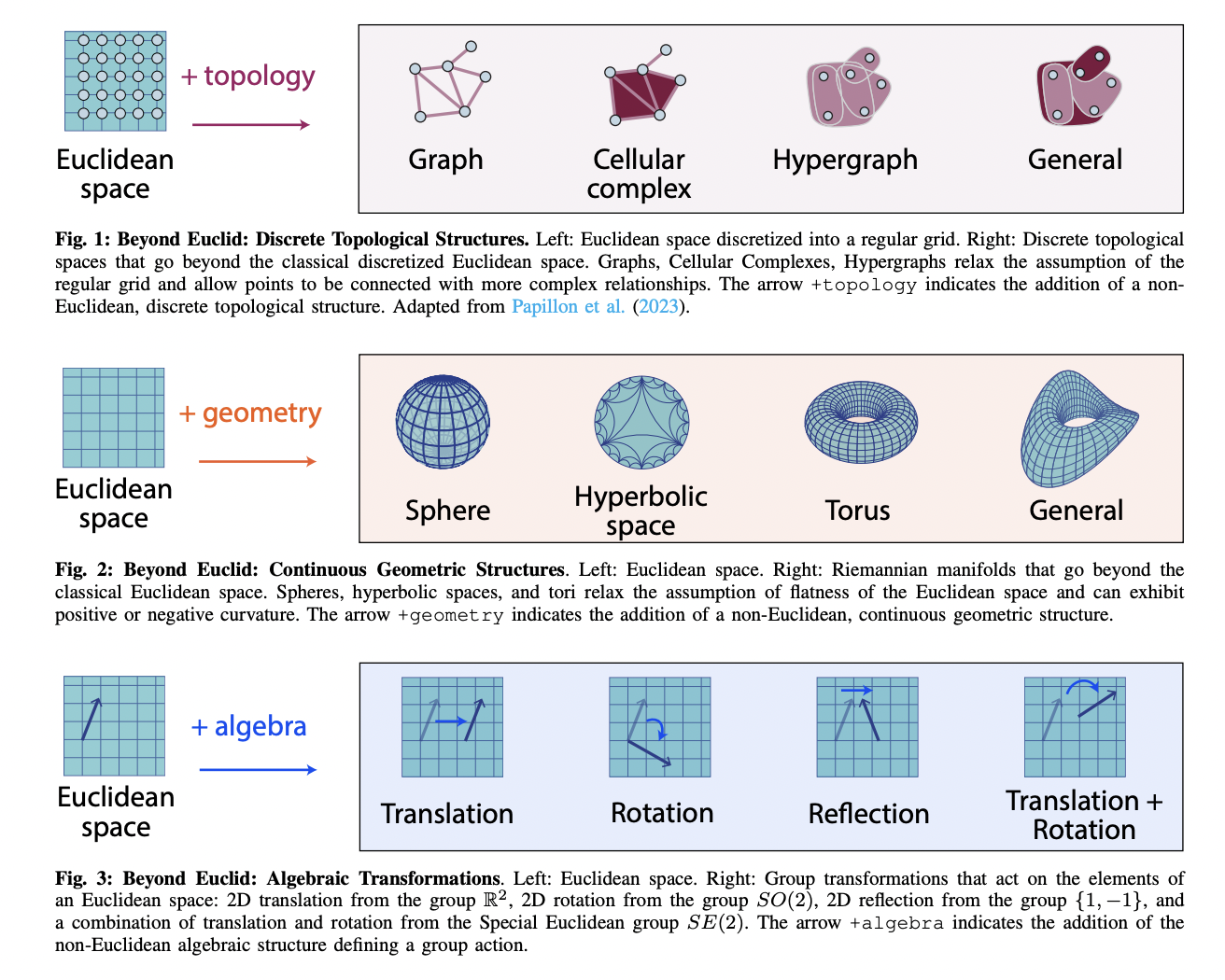
Предложенная методология использует математические основы топологии, геометрии и алгебры для обработки неевклидовых данных. Топология изучает свойства, сохраняющиеся при непрерывных преобразованиях, такие как связность и непрерывность, что критически важно для понимания взаимосвязей в сложных наборах данных. Например, в топологическом анализе данных точки представлены в структурах, таких как графы или гиперграфы, которые описывают сложные взаимосвязи, выходящие за рамки возможностей евклидова пространства.
Геометрия, в частности, риманова геометрия, используется для анализа данных, лежащих на изогнутых многообразиях. Многообразия представляют собой пространства, локально похожие на евклидово пространство, но имеющие глобальную кривизну. Оборудуя эти многообразия римановой метрикой, исследователи могут определить расстояния и углы, что позволяет измерять и анализировать данные. Этот подход особенно полезен в областях компьютерного зрения, где изображения можно рассматривать как сигналы на изогнутых поверхностях, или в нейронауке, где активность мозга отображается на сложные геометрические структуры.
Алгебра предоставляет инструменты для изучения симметрий и инвариантностей данных через групповые действия. Группы, в частности, группы Ли, описывают преобразования, сохраняющие структуру данных, такие как вращения и трансляции. Эта алгебраическая перспектива существенна для задач, требующих инвариантных признаков, например, распознавания объектов в различных ориентациях. Объединяя эти математические инструменты, предложенная методология улучшает способность моделей машинного обучения извлекать знания и генерализировать на неевклидовых пространствах данных.
Данный материал успешно решает ограничения традиционных методов машинного обучения в обработке неевклидовых данных, предлагая комплексную методологию, объединяющую топологию, геометрию и алгебру. Этот подход расширяет область применения машинного обучения и открывает новые возможности для исследований и применения, что делает его значительным прорывом в области. Преодолевая разрыв между классическим машинным обучением и богатыми математическими структурами, лежащими в основе реальных данных, этот подход утрясает путь к новой эре машинного обучения, способного лучше улавливать врожденную сложность мира вокруг нас.
Практическое внедрение ИИ-решений
Если вы хотите, чтобы ваша компания развивалась с помощью искусственного интеллекта (ИИ) и оставалась в числе лидеров, грамотно используйте предложенный план развития машинного обучения с геометрическими, топологическими и алгебраическими структурами. Проанализируйте, как ИИ может изменить вашу работу, определите области применения автоматизации, подберите подходящее решение, внедряйте ИИ решения постепенно, исходя из результатов и KPI, расширяйте автоматизацию на основе данных и опыта.
Для получения советов по внедрению ИИ обращайтесь к нам.
Ознакомьтесь с ИИ-ассистентом в продажах от Flycode.ru, который помогает отвечать на вопросы клиентов, генерировать контент для отдела продаж и снижать нагрузку на первую линию.
Узнайте, как ИИ может изменить ваши процессы с решениями от Flycode.ru.
«`