Улучшение математического мышления в открытых языковых моделях с помощью метода групповой относительной политики оптимизации (GRPO)

“`html

Групповая относительная оптимизация политики (GRPO): улучшение математического мышления в открытых языковых моделях

GRPO – новый метод обучения с подкреплением, представленный в статье DeepSeekMath. Он базируется на фреймворке Proximal Policy Optimization (PPO), разработанный для улучшения математических способностей и снижения потребления памяти. Этот метод предлагает несколько преимуществ, особенно подходящих для задач, требующих продвинутого математического рассуждения.

Внедрение GRPO

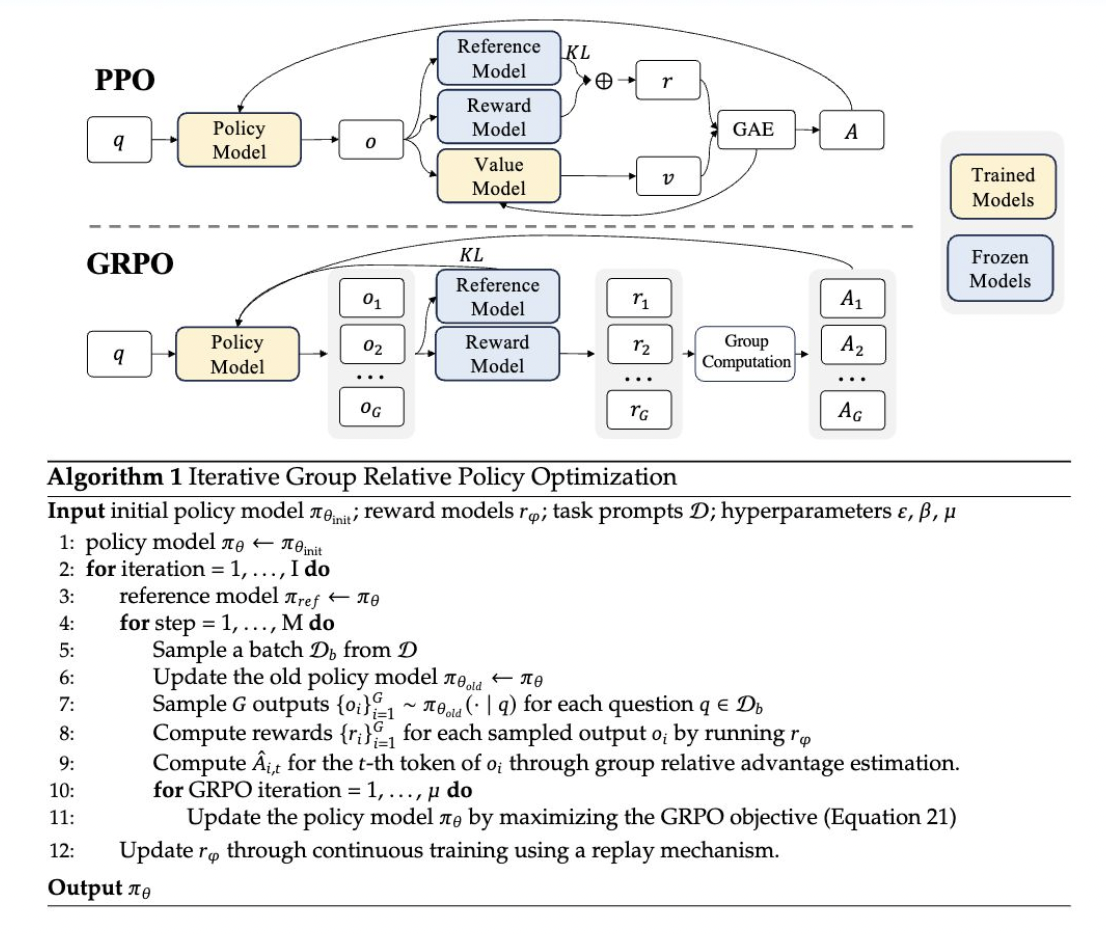
Реализация GRPO включает несколько ключевых этапов:

Генерация результатов: текущая политика генерирует множество результатов для каждого входного вопроса.
Оценка результатов: эти выводы затем оцениваются с использованием модели вознаграждения.
Вычисление преимуществ: средний балл этих вознаграждений используется в качестве базовой линии для вычисления преимуществ.
Обновление политики: политика обновляется с целью максимизации цели GRPO, включающей в себя преимущества и условие дивергенции KL.

Этот подход отличается от традиционного PPO тем, что он устраняет необходимость в модели функции ценности, тем самым уменьшая потребление памяти и вычислительную сложность. Вместо этого GRPO использует групповые баллы для оценки базовой линии, упрощая процесс обучения и требования к ресурсам.

Инсайты и преимущества GRPO

GRPO вводит несколько инновационных особенностей и преимуществ:

Упрощенный процесс обучения: за счет отказа от модели функции ценности и использования групповых баллов GRPO снижает сложность и потребление памяти, typoк которым обычно привязан PPO. Это делает процесс обучения более эффективным и масштабируемым.
Условие дивергенции KL в функции потерь: в отличие от других методов, добавляющих условие дивергенции KL к вознаграждению, GRPO интегрирует это условие непосредственно в функцию потерь. Это позволяет стабилизировать процесс обучения и улучшить производительность.
Улучшение производительности: GRPO продемонстрировал значительное улучшение производительности в математических бенчмарках. Например, он улучшил оценки GSM8K и набора данных MATH примерно на 5%, демонстрируя свою эффективность в улучшении математического рассуждения.

Сравнение с другими методами

GRPO имеет сходство с методом Rejection Sampling Fine-Tuning (RFT), но включает уникальные элементы, отличающие его от других методов. Одним из критических отличий является его итерационный подход к обучению моделей вознаграждения. Этот итерационный процесс помогает более эффективно настраивать модель, постоянно обновляя ее на основе последних выводов политики.

Применение и результаты

GRPO был применен к DeepSeekMath, модели языка, специфичной для области, разработанной для превосходства в математическом рассуждении. Данные обучения с подкреплением составляли 144 000 цепей мысли из набора данных, предварительно настроенного на контролируемую тонкую настройку. Модель вознаграждения, обученная с использованием процесса “Math-Shepherd”, была важна для оценки и направления обновлений политики.

Результаты применения GRPO были многообещающими. DeepSeekMath значительно улучшился в задачах как в пределах, так и вне области во время обучения с подкреплением. Способность метода повысить производительность без использования отдельной модели функции ценности подчеркивает его потенциал для более широкого применения в сценариях обучения с подкреплением.

Заключение

Групповая относительная оптимизация политики (GRPO) значительно продвигает методы обучения с подкреплением, адаптированные для математического рассуждения. Его эффективное использование ресурсов, в сочетании с инновационными методиками вычисления преимуществ и интеграции условия дивергенции KL, позиционирует его как отличный инструмент для улучшения возможностей открытых языковых моделей. Как показано на примере его применения в DeepSeekMath, GRPO может перевести границы того, что могут достичь языковые модели в сложных структурированных задачах, таких как математика.

Источники: