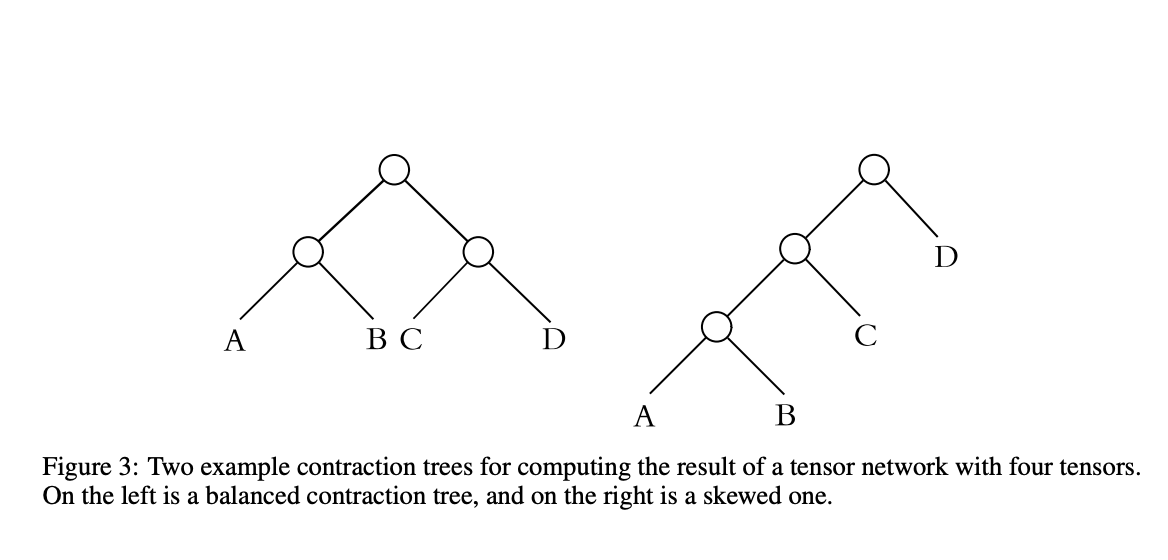
Улучшение путей сокращения тензоров с помощью модифицированного жадного алгоритма с улучшенной функцией затрат
Тензорные противоречия используются для решения проблем, связанных с различными областями исследований, включая подсчет моделей, квантовые цепи, задачи графов и машинное обучение. Но для минимизации вычислительных затрат важно найти порядок противоречий. Результат вычисления произведения последовательности матриц A, B и C всегда будет одинаковым, но вычислительные затраты будут различны в зависимости от размеров матриц. Кроме того, стоимость сокращения тензорных сетей увеличивается с увеличением количества тензоров. Путь, используемый для определения, какие два тензора должны сокращаться друг с другом, важен для улучшения времени вычислений.
Метод поиска эффективного пути
Ранее работы сосредоточены на поиске эффективных путей сокращения тензорных гиперсетей. Для вычисления путей сокращения тензоров одним из существующих методов является использование метода имитации отжига и генетического алгоритма, который превосходит стандартный жадный подход для более маленьких сетей. Второй метод — это разложение графа, в котором используются методы Line-Graph (LG) и Factor-Tree (FT). LG использует структурированный анализ графов для определения порядка сокращения, в то время как FT используется на предварительной обработке для обработки тензоров высокого ранга. Третий метод, в котором комбинируются обучение с подкреплением (RL) и графовые нейронные сети (GNN), используется для поиска эффективного пути, включая реальные и синтетические квантовые цепи.
Команда исследователей предложила новый метод повышения путей сокращения тензоров с использованием модифицированного стандартного жадного алгоритма с улучшенной функцией стоимости. Этот метод превосходит реализации стандартного жадного алгоритма по Optimized Einsum (opt_einsum), и в некоторых случаях он превосходит методы, такие как разбиение гиперграфа в сочетании с жадным методом.
Вычисление путей сокращения тензоров
Исследователи использовали SGA в opt_einsum для эффективного вычисления путей сокращения для большого количества тензоров. Существуют три фазы, в которых вычисляется порядок сокращения:
- Вычисление покомпонентного умножения тензоров с одним и тем же набором индексов.
- Сокращение оставшихся тензоров до тех пор, пока все сокращаемые индексы не истощатся путем выбора пары с наименьшей стоимостью на каждом шаге.
- Вычисление внешних произведений путем выбора пары, минимизирующей сумму размеров входных данных на каждом шаге.
Кроме того, модифицированный жадный алгоритм использует функции стоимости в качестве параметров, в отличие от SGA, который использует только одну функцию стоимости. Затем во время выполнения используются различные функции стоимости, и наиболее подходящая функция стоимости выбирается для дальнейшего вычисления порядка сокращения.
Эксперименты и выводы
Исследователи провели два эксперимента. В первом эксперименте было вычислено 128 путей с каждым алгоритмом для каждого примера проблемы с целью оценки качества решения без учета времени вычислений. Во втором эксперименте ограничение было не на количество путей, а на время вычислений, которое ограничивалось 1 секундой. Цель состояла в том, чтобы показать баланс между временем и качеством для быстрого нахождения эффективного пути для практических сценариев.
В заключение, исследователи предложили новый подход для улучшения путей сокращения тензоров с использованием модифицированного стандартного жадного алгоритма. Используется подход с несколькими функциями затрат, где каждая функция затрат рассчитывается для каждого примера проблемы, и лучшая функция затрат выбирается для вычисления порядка сокращения. В сравнении со стандартными жадными и случайными жадными алгоритмами opt_einsum, и жадным алгоритмом и методом разбиения гиперграфа, предложенный метод может находить эффективные порядки сокращения за меньшее время и решать сложные проблемы, в то время как другие методы не справляются с этой задачей.